A CP Solution for XKCD NP Complete Restaurant Order

I’ve been messing around with Constraint Programming (CP) the past week. A few people at work have tried it out on some real world problems lately but it didn’t seem to stand up when given a lot of data and variables. This seemed sad as the declarative nature of CP attracts me and it strikes me there must be a set problems that it could be used for and it deserved a look.

The first CP model I wrote by myself is stupidly simple but since my non techie fiance understood the code I figure it is a good example. The problem is as described by XKCD below, select some appetizers from the menu so that the total cost adds up to $15.05.

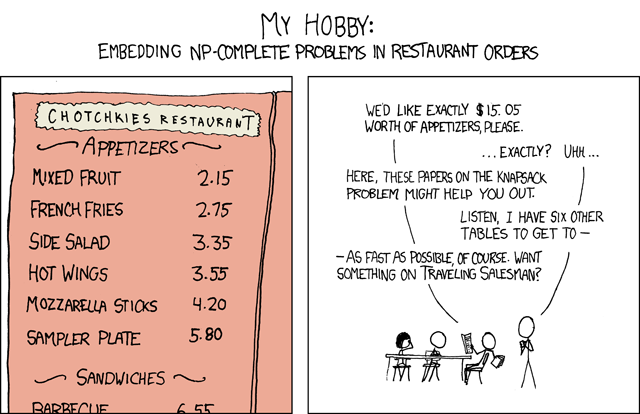
I modeled the problem in Minizinc, a declarative language for modeling CP problems. I am just learning so if you know Minizinc and I’ve done something dumb don’t judge me too harshly.

Firstly we declare a bunch of variables that the solver needs to find values for. We provide the solver a domain in which the variables must lie, zero to ten for all variables in this case. Each of these variables represents the number of times as part of a solution we buy an item to add up to $15.05.

var 0..10: fruit;
var 0..10: fries;
var 0..10: salad;
var 0..10: wings;
var 0..10: sticks;
var 0..10: sampler;

Then we declare a constraint, something that the solver must meet to solve the problem. And in this case we say that a sum of the cost of the items (converted to cents) multiplied by the number of items in the solution must equal the required 1505 cents (that English version could be taken a couple of ways, the maths below makes better sense).

constraint fruit*215 + fries*275 + salad*335 + wings*355 + sticks*420 + sampler*580 == 1505;

We tell the solver to solve to satisfy.

solve satisfy;

And provide a format in which to output the solution.

output ["fruit=", show(fruit), "\t fries=", show(fries),
        "\t salad=", show(salad), "\t wings=", show(wings),
        "\t sticks=", show(sticks), "\t sampler=", show(sampler)];

Running the model gives us:

$ minizinc --all-solutions xkcd.mzn
fruit=7     fries=0     salad=0     wings=0     sticks=0     sampler=0
----------
fruit=1     fries=0     salad=0     wings=2     sticks=0     sampler=1
----------
==========

So there we go, all the possible solutions to the poor waiters problem! We know it is all of the solutions because of the “==========” minizinc cryptically places at the end of its output. Of course this problem is easy to brute force with a couple of for loops, there aren’t that many combinations.

But it is a start along what I hope will be a fruitful path.

Update: as people have noted on HN and Reddit I originally screwed up transcribing the price for salad which produced a couple of extra solutions. Fixed that now.